＿表現が難しかったものを振り返ると、 電気力線や磁力線(48「電気ベクトルと電気力線」、53「電流による磁力線」 いずれも容量オーバーでUP出来ず)や、69「倒立円錐形内側の物体の運動」などがある。(下図)
今回、69「倒立円錐形内側の物体の運動」の作成にあたり電気力線や磁力線の作成時を思い出して積分法で つくってみたので、忘れないうちにその方法を書き留めてみました。
右の図は今回私が作った69「倒立円錐形内側の物体の運動」のグラフ画面(左)とそのDATA画面(右)です。
以下はこのDATAをどのように作成したかについて書いてみることにします。
今回は、円錐上を移動するたびに半径や速度や加速度が同時に変化していき、軌道を単純な関数で表示できそうにない ので、微少時間（⊿ｔ）ごとに諸変化要素を追いかけながらその間は等加速度運動をするとして軌道を積み上げて行く
方法（積分法）を取り入れてみた。物体と円錐内壁との摩擦は無いものとして考えました。
下の図は基本となる力と速度に関する考えを図にしたものです。これに力学的エネルギー保存の法則を併せ、⊿ｔで移動 するχとｈを求めていくことにします。
ｔ＝０では αy0＝ｇSinθ－υχ0^2×Cosθ/R 初速度υy0
ｔ＝⊿ｔ×i では αyi＝ｇSinθ－υχi^2×Cosθ/ｒi＝Sinθ(ｇ－υχi^2/ｈi） ・・・①
υｙi＝υｙ(i－１)＋αyi⊿ｔ ・・・・・・・・②
⊿ｙi＝υｙ(i－１)⊿ｔ＋αyi⊿ｔ^2/２ ・・・③ となり、
また、力学的エネルギー保存の法則
ｍ(υχ0^2＋υｙ0^2）/２＋ｍｇｈ0＝
ｍ(υχi^2＋υｙi^2）/２＋ｍｇｈi より、
υχi^2＝υχ0^2＋υｙ0^2－υｙi^2＋２ｇ(ｈ0―ｈi) ・・・④
となります。
これをDATA表に仕上げます。
まず、右図のように定数を設定します。黄色セルにはスピンボタンで数値を書き込みます。水色セルが真の定数です。
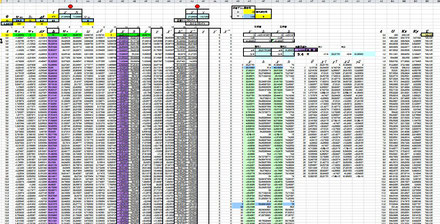
次に下の図のようにｔ、αy、υｙ、⊿ｙi、ｈ、υχ、ｒ、ω、⊿Θ、Θ、χ 列
の各３７行目に関数を書き込みこれを500行までコピーしました。３６行目はそれぞれの初期値を設定します。
３６行の緑や黄色セルは３７行とは違った関数や数値が入っているので注意してください。関数を見て理解してください。
今回は⊿ｔに0.2を設定（W33=20)したので、500行で92.8秒間（T500＝92.8）のDATAが完成しました。
あとはタイマーで発生する時刻をもとにそれ以前のDATAを表示させると同時に、 VLOOKUP関数で赤い球体の時刻ごとの座標を表示させればほぼ完成です。
後は散布グラフでχとｈを軌跡（青線）に、赤い球体を時刻の座標に設定すれば終わりです。（今回は上から見た図と鳥瞰図をオプションでつけてあります。）
このように、⊿ｔごとに変化するデータを積み重ねてその変化を追う方法なので、⊿ｔが限りなく０に近いほど真の変化に近付きますが⊿ｔが大きいと遠似的な物となってしまいます。
実際、53「電流による磁力線」では円にならず螺旋になってしまいました。